Apa Elastisitas itu?

Elastisitas merupakan suatu sifat bahan yang dapat berubah baik dalam ukuran maupun bentuk setelah mendapat gaya luar, tetapi benda itu akan kembali ke ukuran dan bentuk semula setelah gaya luar itu di tiadakan.

Stress, Strain, dan Modulus Young

Tegangan (Stress) menyatakan perbandingan antara gaya dengan luasan yang mendapat gaya, bila dinyatakan dalam persamaan ditulis sebagai $displaystyle sigma =frac{F}{A}$ . Dengan $sigma$ adalah tegangan $displaystyle N/m^{2}$, F adalah gaya (N) dan A adalah luas bidang yang dikenai gaya ($m^{2}$).

Perhatikan gambar sebuah percobaan pada satu buah pegas mula-mula panjangnya 30 cm, pada percobaan pertama diujung pegas diberi satu buah beban kuningan dengan berat 30 N pegas bertambah panjangnya sebesar 5 cm.

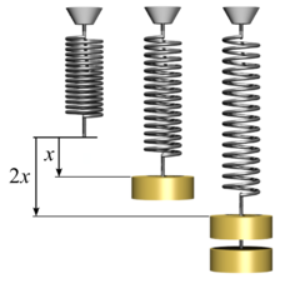
Percobaan berikutnya ujung pegas yang sama diberi dua buah kuningan maka berat beban yang ditanggung oleh pegas adalah 2 x 30 N. Setelah diukur Panjang pegas menjadi 40 cm atau bertambah sebesar 2x 5cm dari percobaan pertama. Kemudian hasil percobaan itu dituliskan dalam grafik seperti dibawah ini.

Perbandingan antara beban dan perubahan panjang pegas dituliskan pada tabel berikut

Hukum Hooke

Hukum Hooke menyatakan bahwa pada daerah elastis suatu benda, besarnya pertambahan panjang sebanding dengan gaya yang bekerja pada benda itu.
Selanjutnya dapat ditulis $F=k.Delta x$

Hubungan antara gaya yang meregangkan pegas dan pertambaahan panjangnya pada daerah elastis pertama kali diselidiki oleh Robert Hooke (1635-1703). hasil penyelidikannya dinyatakan dalam sebuah hukum yang dikenal dengan hukum Hooke, yang menyatakan bahwa pada daerah elastis suatu benda, besarnya pertambahan panjang sebanding dengan gaya yang bekerja pada benda itu.
Selanjutnya dapat ditulis. 

persamaan tersebut menunjukkan bahwa perubahan panjang benda sebanding dengan gaya yang diberikan, yang nilainya dinyatakan dengan konstanta pegas (k). Sesuai hukum Newton III, maka gaya beban pada bahan kenyal akan mendapat reaksi berupa gaya F yang besarnya sama tetapi arhanya berlawanan.
F(x) = -k. ∆x (ada tanda NEGATIF)

Susunan Pegas

Pegas Disusun Seri

Pegas satu memiliki konstanta k1, pegas kedua memiliki konstanta k2, dan pegas ketiga memiliki konstanta k3, jika ketiganya disusun seri, maka secara keseluruhan memiliki konstanta gabungan yang sebut saja konstanta seri dengan simbol ks. Ketika pegas yang diseri salah satu ujungnya ditarik seperti gambar, maka masing-masing pegas akan bertambah Panjang besar pertambahan panjang akhir dari susunan pegas tersebut adalah jumlah pertambahan panjang ketiga pegas tersebut.
∆X = ∆X1 + ∆X2 + ∆X3

Pegas Disusun Pararel

Pegas satu memiliki konstanta k1, pegas kedua memiliki konstanta k2, dan pegas ketiga memiliki konstanta k3, jika ketiganya disusun paralel, maka ketika ditarik dengan gaya F ketiga pegas akan mengalami pertambahan panjang sama besar. Gaya F terdistribusi pada ketiga pegas dengan besar masing masing F1, F2, dan F3.

Persamaan tersebut menunjukkan hubungan nilai konstanta susunan pegas parelal (kp) dengan konstanta masing-masing pegas (k1, k2, dan k3). Dengan penjumlahan seperti itu, nilai kp akan lebih besar dari pada masing-masing nilai k penyusunnya. Yang artinya bahwa pegas yang disusun paralel akan menjadi sistem pegas yang lebih sukar diubah bentuk dan ukurannya.

Energi Potensial Pegas

Sebuah pegas yang ditarik akan cenderung kembali ke keadaan semula apabila tarikannya dilepas. Kecenderungan ini menjadikan pegas memiliki energi ketika ditarik. Energi yang dimiliki pegas ketika pegas ditarik atau ditekan dikenal dengan besaran energi potensial pegas.

Usaha yang dilakukan sebuah gaya dapat diilustrasikan dengan luasan daerah dibawah grafik F – ∆x seperti ditunjukkan gambar berikut :

Grafik F-∆x pada pegas yang ditarik adalah sebagai berikut :

Dimana bentuk daerah dibawah grafik adalah berupa segitiga, sehingga usaha yang dilakukan gaya F pada pegas besarnya sama dengan luas daerah segitiga tersebut.

Persamaan tersebut menunjukkan bahwa energi potensial pegas (Ep) dipengaruhi oleh perubahan panjang dari pegas itu sendiri, jika perubahan pegas (∆x) diperbesar, maka pegas akan memiliki energi yang makin besar.